Chapter 5 Use case 3: joint_model() with multiple traditional gear types
This third use case will show how to fit and interpret the joint model with paired eDNA and traditional survey data when multiple traditional gear types have been used. These different gear types may have different expected catch rates, \(\mu\), represented by gear-specific scaling coefficients q.
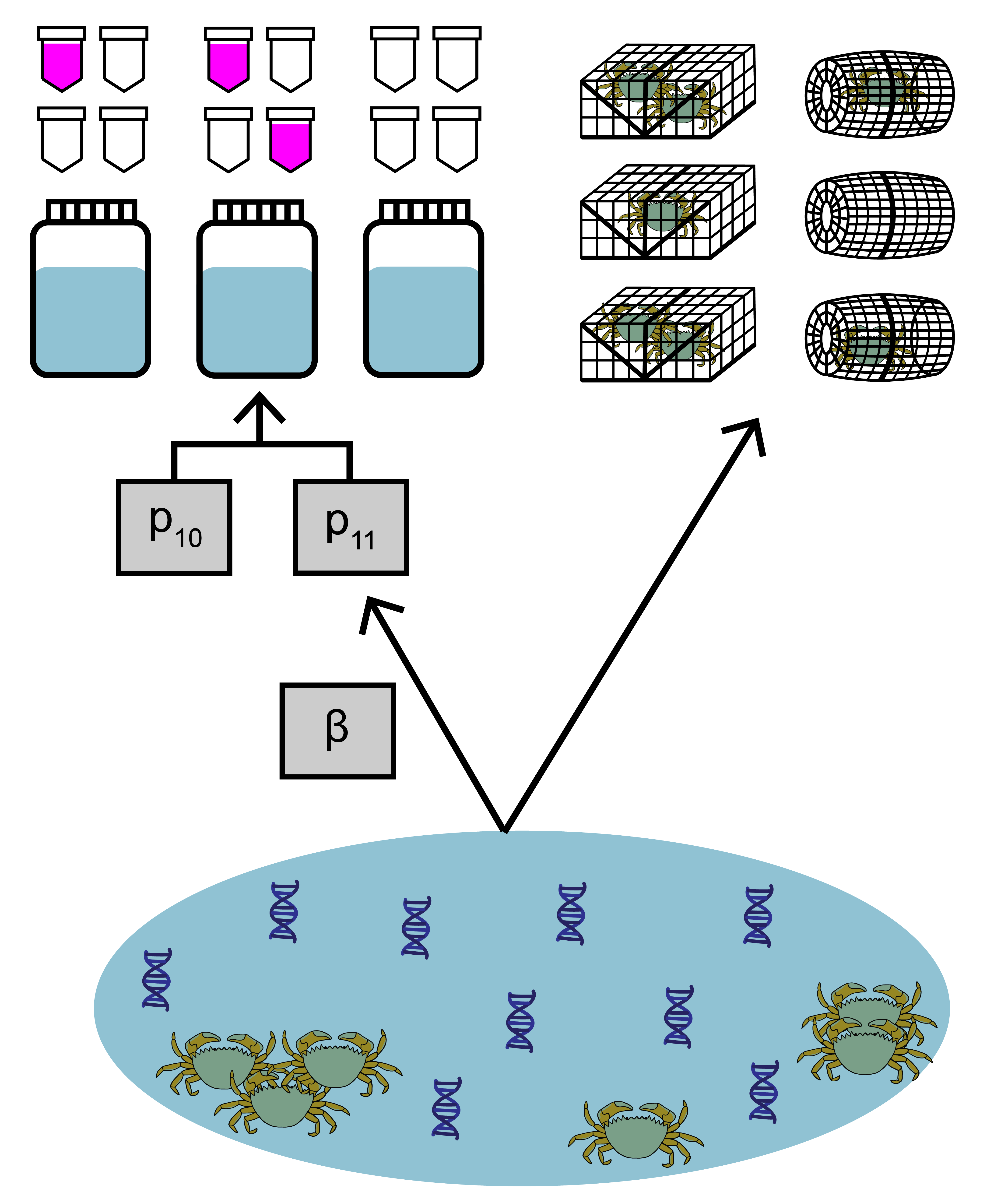
The data used in this example comes from a study by Keller et al. (2022) about invasive European green crab (Carcinus maenas) in Washington state. Environmental DNA samples were collected at 20 sites, along with paired baited trap sampling. The eDNA data is detection/non-detection data generated through quantitative polymerase chain reaction (qPCR).
5.1 Prepare the data
Similar to the goby data, the green crab data is still a list of matrices. Now, instead of data on site-level covariates, site_cov, there is data representing the gear type for each of the traditional samples, count_type.
## [1] "pcr_n" "pcr_k" "count" "count_type"Again, all matrices should have the same number of rows (n=20), and rows across all four matrices should correspond to the same sites.
Let’s look at the count. This data is from baited trap sampling for green crab. Each integer refers to the catch of each trap (i.e., catch per unit effort, when effort = 1). The rows correspond to sites, and the columns refer to the replicated trap samples (secondary sample units) at each site, with a maximum of 420 samples.
## [1] 20 420Blank spaces are filled with NA at sites where fewer trap samples were collected than the maximum. In this example, the count data are integers, but continuous values can be used in the model (see Eq. 1.3 in the model description).
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
## [1,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
## [2,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
## [3,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
## [4,] 1 0 1 2 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 1
## [5,] 0 0 0 0 0 0 0 0 NA NA NA NA NA NA NA NA NA NA NA NA
## [6,] 0 0 0 0 0 0 NA NA NA NA NA NA NA NA NA NA NA NA NA NANext, let’s look at count_type, which consists of integer indicators of gear type for each trap sample. Here, 1 refers to the Fukui gear type, and 2 refers to the Minnow gear type.
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
## [1,] 1 1 1 1 2 1 2 2 2 2 2 2 1 1 1 1 2 1 1 2
## [2,] 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 2 2 2 2
## [3,] 1 1 1 2 1 2 1 1 1 2 1 2 2 1 2 2 1 2 1 2
## [4,] 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2
## [5,] 1 2 1 2 1 2 1 2 NA NA NA NA NA NA NA NA NA NA NA NA
## [6,] 2 1 2 1 2 1 NA NA NA NA NA NA NA NA NA NA NA NA NA NANote that the locations of the NAs in this matrix match count.
For more data formatting guidance, see section 2.1.1.
5.2 Fit the model
Now that we understand our data, let’s fit the joint model. The key arguments of this function include:
- data: list of
pcr_k,pcr_n,count, andcount_typematrices - cov: no site-level covariates are included in this model
- family: probability distribution used to model the trap count data. A negative binomial distribution is chosen here.
- p10_priors: Beta distribution parameters for the prior on the probability of false positive eDNA detection, \(p_{10}\). c(1, 20) is the default specification.
- q: logical value indicating the presence of multiple traditional gear types.
More parameters exist to further customize the MCMC sampling, but we’ll stick with the defaults.
5.3 Model selection
We previously made a choice to model the green crab count data with a negative binomial distribution. Perhaps we want to test how that model specification compares to a model specification where count data is modeled with a poisson distribution.
# run the joint model with poisson distribution
greencrab_fit_q_pois <- joint_model(data = green_crab_data, cov = NULL,
family = "poisson", p10_priors = c(1, 20),
q = TRUE)Let’s also fit some models where we assume that both gear types have the same catchability. We set q = FALSE to not estimate gear scaling coefficients.
# run the joint model with four covariates
greencrab_fit_negbin <- joint_model(data = green_crab_data, cov = NULL,
family = "negbin", p10_priors = c(1, 20),
q = FALSE)
greencrab_fit_pois <- joint_model(data = green_crab_data, cov = NULL,
family = "poisson", p10_priors = c(1, 20),
q = FALSE)Now let’s perform model selection using leave-one-out cross validation.
# perform model selection
joint_select(
model_fits = list(
# include gear scaling coefficient, model count data with negative binomial
greencrab_fit_q_negbin$model,
# include gear scaling coefficient, model count data with poisson
greencrab_fit_q_pois$model,
# include gear scaling coefficient, model count data with negative binomial
greencrab_fit_negbin$model,
# include gear scaling coefficient, model count data with poisson
greencrab_fit_pois$model
)
)## elpd_diff se_diff
## model3 0.0 0.0
## model1 -1.3 2.0
## model4 -166.1 38.5
## model2 -168.3 37.6These results tell us that models one and three (models with and without gear scaling coefficients for the gear types) that use a negative binomial distribution for count data have similar Bayesian LOO estimates of the expected log pointwise predictive density (elpd_loo). Notably, a negative binomial distribution represents the data-generating process for our count data much better than a poisson distribution.
5.4 Interpret the output
5.4.1 Summarize posterior distributions
For the sake of illustration, let’s interpret the results of the model fit with gear scaling coefficients. Use joint_summarize() to see the posterior summaries of the model parameters.
## mean se_mean sd 2.5% 97.5% n_eff Rhat
## p10 0.019 0.000 0.010 0.005 0.042 9155.422 1
## alpha[1] 1.271 0.003 0.244 0.798 1.763 8264.929 1
## q[1] 0.779 0.001 0.100 0.598 0.991 6636.986 1This summarizes the mean, standard deviation (sd), and quantiles of the posterior estimates of \(p_{10}\), \(\alpha\), and \(q\), as well as the effective sample size (n_eff) and \(\hat{R}\) (Rhat) for the parameters. More informative about effective sample size and \(\hat{R}\) can be found in the algorithm convergence section, but briefly, the \(\hat{R}\) value is the frequently used statistic for assessing model convergence. We typically want \(\hat{R}\) to be less than 1.05, so it looks like our model converged.
The mean estimated probability of a false positive eDNA detection is ~0.01, and the 2.5% and 97.5% quantiles show the bounds of the 95% credibility interval (the equal tailed credibility interval, to be specific.)
q[1] represents the gear scaling coefficient of gear type 2, which scales the catch rate of gear type 2 relative to gear type 1. \(\alpha\) are regression coefficients that scale the sensitivity of eDNA relative to traditional sampling. Since there were no site-level covariates in this model, \(\alpha\) is just a scalar, intercept term (see Eq. 4 in model description).
The parameter \(\beta_i\) represents the site-specific sensitivity of eDNA relative to traditional sampling. We use \(i\) to index the sites. Since we don’t have any site-level covariates here, \(\beta\) is equal at all sites and equal to \(\alpha_1\). For example, here are the first few \(\beta_i\):
## mean se_mean sd 2.5% 97.5% n_eff Rhat
## alpha[1] 1.271 0.003 0.244 0.798 1.763 8264.929 1
## beta[1] 1.271 0.003 0.244 0.798 1.763 8264.929 1
## beta[2] 1.271 0.003 0.244 0.798 1.763 8264.929 1
## beta[3] 1.271 0.003 0.244 0.798 1.763 8264.929 1
## beta[4] 1.271 0.003 0.244 0.798 1.763 8264.929 1
## beta[5] 1.271 0.003 0.244 0.798 1.763 8264.929 1Now let’s look at the summary of mu.
## mean se_mean sd 2.5% 97.5% n_eff Rhat
## mu[1,1] 0.107 0.000 0.028 0.060 0.169 12238.772 1
## mu[1,2] 0.083 0.000 0.022 0.046 0.134 11789.846 1
## mu[2,1] 0.033 0.000 0.035 0.001 0.128 13125.266 1
## mu[2,2] 0.025 0.000 0.027 0.001 0.100 13000.401 1
## mu[3,1] 0.017 0.000 0.017 0.000 0.063 13634.825 1
## mu[3,2] 0.013 0.000 0.013 0.000 0.048 13631.934 1
## mu[4,1] 0.683 0.001 0.109 0.493 0.915 10156.163 1
## mu[4,2] 0.529 0.001 0.090 0.374 0.725 12773.877 1
## mu[5,1] 0.100 0.001 0.107 0.002 0.393 12022.105 1
## mu[5,2] 0.077 0.001 0.082 0.002 0.304 12148.578 1
## mu[6,1] 0.120 0.001 0.131 0.003 0.491 11718.438 1
## mu[6,2] 0.093 0.001 0.101 0.002 0.372 12097.780 1
## mu[7,1] 0.013 0.000 0.013 0.000 0.047 13330.308 1
## mu[7,2] 0.010 0.000 0.010 0.000 0.036 13510.335 1
## mu[8,1] 0.306 0.003 0.286 0.011 1.070 12003.430 1
## mu[8,2] 0.237 0.002 0.222 0.009 0.824 12439.594 1
## mu[9,1] 0.034 0.000 0.032 0.001 0.122 12694.594 1
## mu[9,2] 0.026 0.000 0.025 0.001 0.093 12735.789 1
## mu[10,1] 1.056 0.002 0.246 0.648 1.617 10362.615 1
## mu[10,2] 0.816 0.002 0.188 0.502 1.246 13492.170 1
## mu[11,1] 0.300 0.003 0.277 0.013 1.016 11439.695 1
## mu[11,2] 0.232 0.002 0.214 0.010 0.793 11590.632 1
## mu[12,1] 0.021 0.000 0.021 0.001 0.077 13951.604 1
## mu[12,2] 0.016 0.000 0.016 0.000 0.060 14411.235 1
## mu[13,1] 7.764 0.014 1.352 5.478 10.793 9445.122 1
## mu[13,2] 5.992 0.009 0.990 4.329 8.201 12918.127 1
## mu[14,1] 0.120 0.000 0.020 0.085 0.164 9289.844 1
## mu[14,2] 0.093 0.000 0.016 0.065 0.127 13456.487 1
## mu[15,1] 0.769 0.005 0.550 0.107 2.186 11421.875 1
## mu[15,2] 0.596 0.004 0.429 0.081 1.689 11745.586 1
## mu[16,1] 3.850 0.007 0.658 2.724 5.277 8775.260 1
## mu[16,2] 2.969 0.004 0.463 2.170 3.972 15038.764 1
## mu[17,1] 0.163 0.002 0.183 0.003 0.658 11873.064 1
## mu[17,2] 0.127 0.001 0.142 0.003 0.522 12278.210 1
## mu[18,1] 3.356 0.012 1.091 1.763 5.998 8343.652 1
## mu[18,2] 2.595 0.009 0.846 1.368 4.695 9455.326 1
## mu[19,1] 3.973 0.008 0.734 2.802 5.616 9280.795 1
## mu[19,2] 3.073 0.005 0.576 2.139 4.384 11602.479 1
## mu[20,1] 0.119 0.001 0.070 0.025 0.290 12522.141 1
## mu[20,2] 0.092 0.000 0.054 0.019 0.229 12826.913 1mu[1,1] corresponds to the expected catch rate at site 1 with gear type 1. mu[1,2] corresponds to the expected catch rate at site 1 with gear type 2. mu[2,1] corresponds to the expected catch rate at site 2 with gear type 1.
We can also use functions from the bayesplot package to examine the posterior distributions and chain convergence.
First let’s look at the posterior distribution for \(p_{10}\).
library(bayesplot)
# plot posterior distribution, highlighting median and 80% credibility interval
mcmc_areas(as.matrix(greencrab_fit_q_negbin$model), pars = "p10", prob = 0.8)
Next let’s look at chain convergence for \(p_{10}\) and \(\alpha_1\).
# this will plot the MCMC chains for p10 and alpha
mcmc_trace(rstan::extract(greencrab_fit_q_negbin$model, permuted = FALSE),
pars = c("p10", "alpha[1]"))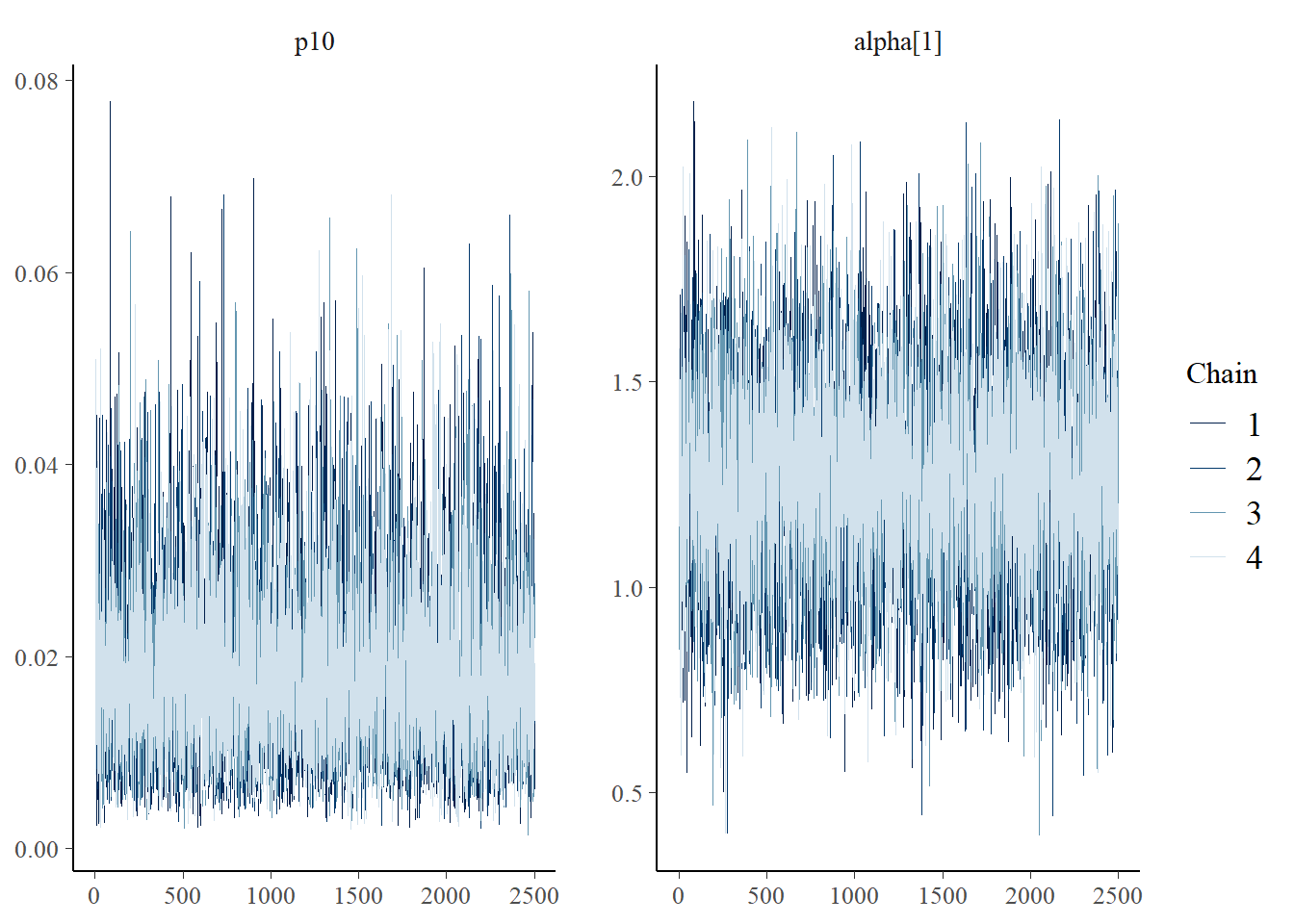
These trace plots show that the algorithm has converged. The chains are overlapping and stationary (i.e., are moving around the same mean and have a constant variance). See more about trace plots in the algorithm convergence section.
5.4.2 Effort necessary to detect presence
To further highlight these results, we can use detection_calculate() to find the units of survey effort necessary to detect presence of the species. This function is finding the median number of survey units necessary to detect species presence if the expected catch rate, \(\mu\) is 0.1, 0.5, or 1. \(\mu\) now represents the expected catch rate of gear type 1.
## mu n_traditional_1 n_traditional_2 n_eDNA
## [1,] 0.1 25 32 28
## [2,] 0.5 6 8 6
## [3,] 1.0 4 5 4We can see that it takes 27 eDNA samples, 25 trap samples (gear type 1), and 31 trap samples (gear type 2) to detect green crab presence with 0.9 probability if the expected catch rate with gear type 1 is 0.1.
We can also plot these comparisons. mu_min and mu_max define the x-axis in the plot and represent the expected catch rate of gear type 1.
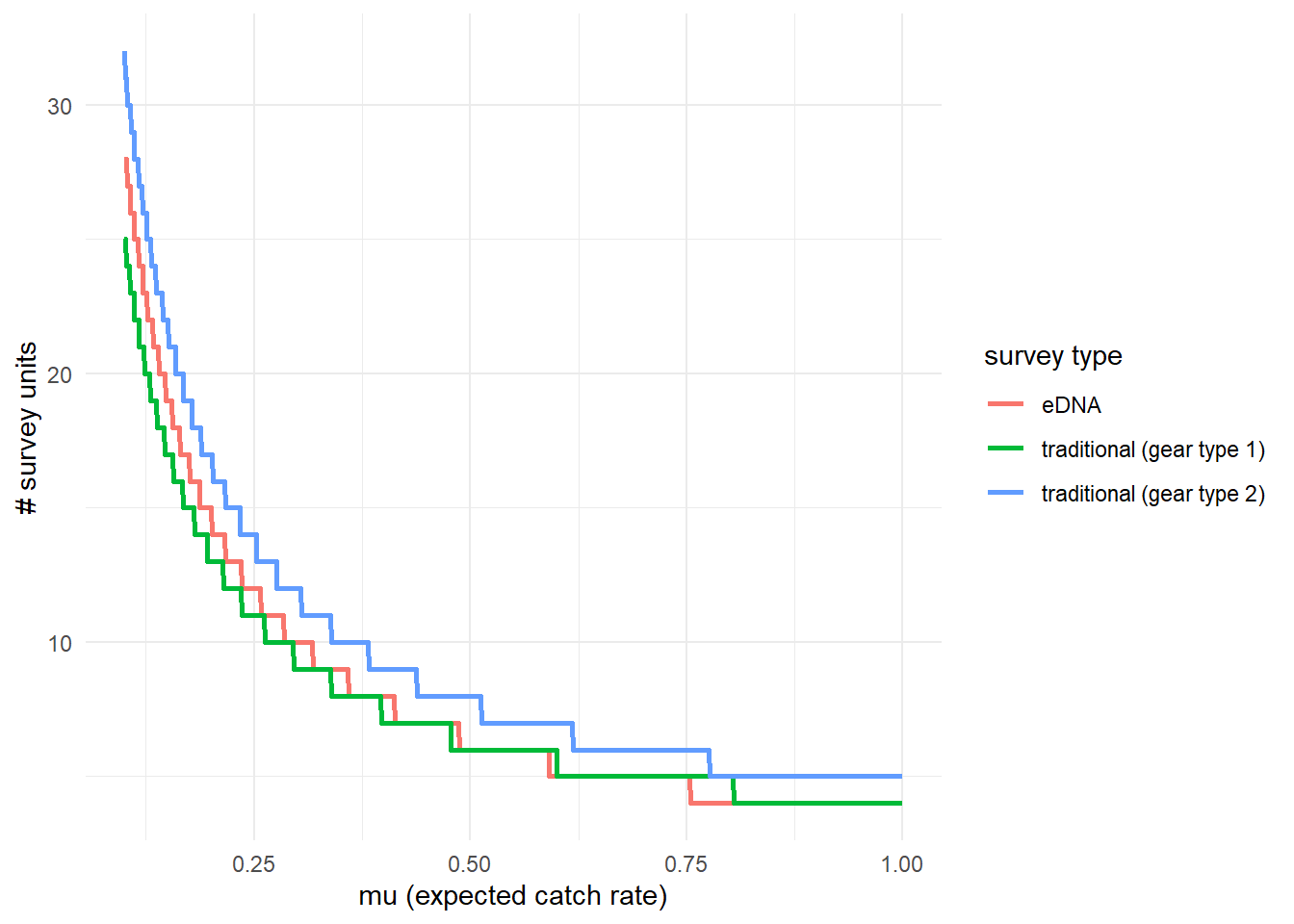
5.4.3 Calculate \(\mu_{critical}\)
Now let’s calculate \(\mu_{critical}\), which is the value of \(\mu\) where the probability of a false positive eDNA detection equals the probability of a true positive eDNA detection.
## gear_1 gear_2
## median 0.05958688 0.046148768
## lower_ci 0.01023755 0.007750009
## upper_ci 0.13601281 0.104339548This function calculates \(\mu_{critical}\) using the entire posterior distributions of parameters from the model, and ‘HDI’ corresponds to the 90% credibility interval calculated using the highest density interval. The first column corresponds to \(\mu_{critical}\) if gear type 1 is used, and the second columns corresponds to \(\mu_{critical}\) if gear type 2 is used.
5.5 traditional_model()
In some circumstances, it may be helpful to model just the traditional survey data without eDNA data for comparison. Use traditional_model here, which requires the following parameters:
- data: list of
countand (optionally)count_typematrices - family: probability distribution used to model the trap count data. A negative binomial distribution is chosen here.
- q: logical value indicating the presence of multiple traditional gear types.
More parameters exist to further customize the MCMC sampling, but we’ll stick with the defaults.
5.6 Initial values
By default, eDNAjoint will provide initial values for parameters estimated by the model, but you can provide your own initial values if you prefer. Here is an example of providing initial values for parameters, mu,p10, alpha, and q, as an input in joint_model().
# set number of chains
n_chain <- 4
# number of sites
nsites <- dim(green_crab_data$count)[1]
# number of gear types
ngear <- sum(!is.na(unique(as.vector(green_crab_data$count_type))))
# initial values should be a list of named lists
inits <- list()
for (i in 1:n_chain) {
inits[[i]] <- list(
# length should equal the number of sites for each chain
mu = stats::runif(nsites, 0.01, 5),
# length should equal 1 for each chain
p10 = stats::runif(1, 0.0001, 0.08),
# length should equal 1 for each chain,
# since there are no site-level covariates
alpha = stats::runif(1, 0.05, 0.2),
# length should equal the number of gear types - 1
q = stats::runif(ngear - 1, 0.5, 1.5)
)
}# now fit the model
fit_inits <- joint_model(data = green_crab_data,
q = TRUE, initial_values = inits,
multicore = TRUE)## $chain1
## $chain1$mu_trad
## [1] 0.68934574 4.98237099 2.21341661 0.93767820 0.39009160 2.67434984
## [7] 4.17259747 1.90818812 0.94145710 4.37582686 3.72914351 0.67206745
## [13] 2.59470689 3.52049060 0.80547956 4.08151647 0.06525918 3.49431579
## [19] 0.49166524 0.76940513
##
## $chain1$mu
## [1] 0.68934574 4.98237099 2.21341661 0.93767820 0.39009160 2.67434984
## [7] 4.17259747 1.90818812 0.94145710 4.37582686 3.72914351 0.67206745
## [13] 2.59470689 3.52049060 0.80547956 4.08151647 0.06525918 3.49431579
## [19] 0.49166524 0.76940513
##
## $chain1$log_p10
## [1] -2.948921
##
## $chain1$alpha
## [1] 0.131938
##
## $chain1$q_log
## log(initial_values[[i]]$q)
## 1 -0.3138776
##
## $chain1$p_dna
## numeric(0)
##
## $chain1$p11_dna
## numeric(0)
##
##
## $chain2
## $chain2$mu_trad
## [1] 2.2396845 3.5493845 4.8195951 0.1471801 0.8179000 1.5418522 1.2482253
## [8] 1.5715238 2.7112179 2.0110080 4.5044049 4.1390190 0.7559088 0.2489318
## [15] 4.5311378 2.9129750 4.4934848 2.3545963 1.6677491 1.7948448
##
## $chain2$mu
## [1] 2.2396845 3.5493845 4.8195951 0.1471801 0.8179000 1.5418522 1.2482253
## [8] 1.5715238 2.7112179 2.0110080 4.5044049 4.1390190 0.7559088 0.2489318
## [15] 4.5311378 2.9129750 4.4934848 2.3545963 1.6677491 1.7948448
##
## $chain2$log_p10
## [1] -2.669912
##
## $chain2$alpha
## [1] 0.1664363
##
## $chain2$q_log
## log(initial_values[[i]]$q)
## 1 -0.3057146
##
## $chain2$p_dna
## numeric(0)
##
## $chain2$p11_dna
## numeric(0)
##
##
## $chain3
## $chain3$mu_trad
## [1] 3.6826252 1.0960775 4.0738423 2.9808043 1.8771174 3.2827205 4.0330430
## [8] 2.6260903 0.5893598 0.3588872 4.9820997 2.9618058 1.0033384 4.6105985
## [15] 1.9924889 3.9738314 4.9823702 0.5733681 0.2572072 3.8329523
##
## $chain3$mu
## [1] 3.6826252 1.0960775 4.0738423 2.9808043 1.8771174 3.2827205 4.0330430
## [8] 2.6260903 0.5893598 0.3588872 4.9820997 2.9618058 1.0033384 4.6105985
## [15] 1.9924889 3.9738314 4.9823702 0.5733681 0.2572072 3.8329523
##
## $chain3$log_p10
## [1] -2.628315
##
## $chain3$alpha
## [1] 0.1426665
##
## $chain3$q_log
## log(initial_values[[i]]$q)
## 1 0.319268
##
## $chain3$p_dna
## numeric(0)
##
## $chain3$p11_dna
## numeric(0)
##
##
## $chain4
## $chain4$mu_trad
## [1] 0.01123538 0.08011821 1.33623996 1.21443434 3.93958515 3.86223142
## [7] 3.64176087 4.41673662 0.40178355 4.93546997 1.87184717 0.19006483
## [13] 3.98611270 1.01334049 4.54937113 2.90028743 2.85671563 0.99226975
## [19] 2.80542847 0.84526245
##
## $chain4$mu
## [1] 0.01123538 0.08011821 1.33623996 1.21443434 3.93958515 3.86223142
## [7] 3.64176087 4.41673662 0.40178355 4.93546997 1.87184717 0.19006483
## [13] 3.98611270 1.01334049 4.54937113 2.90028743 2.85671563 0.99226975
## [19] 2.80542847 0.84526245
##
## $chain4$log_p10
## [1] -3.70818
##
## $chain4$alpha
## [1] 0.163417
##
## $chain4$q_log
## log(initial_values[[i]]$q)
## 1 -0.3096095
##
## $chain4$p_dna
## numeric(0)
##
## $chain4$p11_dna
## numeric(0)