Chapter 4 Use case 2: joint_model() with site-level covariates
This second use case uses the same goby data as in use case 1, except this time we will include site-level covariates that affect the sensitivity of eDNA relative to traditional surveys.
4.1 Site-level covariate data
In addition to count and qPCR data, the goby data includes site-level covariates, which is optional when implementing joint_model(). Here, the data represent salinity, mean time to filter eDNA samples, density of other fish, habitat size, and vegetation presence at each site. Two important notes:
Notice that the continuous covariate data is normalized. This is useful since this data will be used in a linear regression, and it helps algorithm stability for all covariate data to be on the same scale. Similarly, one should use dummy variables for categorical variables (like the “Veg” variable).
The columns in the matrix should be named, since these identifiers will be used when fitting the model.
## Salinity Filter_time Other_fishes Hab_size Veg
## [1,] -0.7114925 -1.17 -0.4738419 -0.2715560 0
## [2,] -0.2109183 -1.24 -0.4738419 -0.2663009 0
## [3,] -1.1602831 -1.29 -0.4738419 -0.2717707 0
## [4,] -0.5561419 0.11 0.5479118 -0.2164312 1
## [5,] -0.9876713 -0.70 0.2437353 4.9981956 1
## [6,] 1.2562818 -0.55 -0.3512823 -0.2934710 0One way to normalize your covariate data:
\[ \frac{x-\mu}{\sigma} \]
For more data formatting guidance, see section 2.1.1.
4.2 Fit the model
Now that we understand our data, let’s fit the joint model. The key arguments of this function include:
- data: list of
pcr_k,pcr_n,count, andsite_covmatrices - cov: character vector of site-level covariates (this model will only include mean eDNA sample filter time and salinity)
- family: probability distribution used to model the seine count data. A poisson distribution is chosen here.
- p10_priors: Beta distribution parameters for the prior on the probability of false positive eDNA detection, \(p_{10}\). c(1,20) is the default specification. More on this later.
- q: logical value indicating the presence of multiple traditional gear types. Here, we’re only using data from one traditional method.
More parameters exist to further customize the MCMC sampling, but we’ll stick with the defaults.
# run the joint model with two covariates
goby_fit_cov1 <- joint_model(data = goby_data,
cov = c("Filter_time", "Salinity"),
family = "poisson", p10_priors = c(1, 20),
q = FALSE, multicore = TRUE)goby_fit_cov1 is a list containing:
- model fit (
goby_fit_cov1$model) of the class ‘stanfit’ and can be accessed and interpreted using all functions in the rstan package. - initial values used for each chain in MCMC (
goby_fit_cov1$inits)
4.3 Model selection
We previously made a choice to include two site-level covariates. Perhaps we want to test how that model specification compares to a model specification with different site-level covariates.
# fit a new model with one site-level covariate
goby_fit_cov2 <- joint_model(data = goby_data, cov = "Veg",
family = "poisson", p10_priors = c(1, 20),
q = FALSE, multicore = TRUE)We can now compare the fit of these model to our data using the joint_select() function, which performs leave-one-out cross validation with functions from the loo package.
## elpd_diff se_diff
## model1 0.0 0.0
## model2 -53.7 31.6These results tell us that model1 has a higher Bayesian LOO estimate of the expected log pointwise predictive density (elpd_loo). This means that goby_fit_cov1 is likely a better fit to the data.
You could keep going with this further and include/exclude different covariates, or compare to a null model without covariates.
4.4 Interpret the output
4.4.1 Summarize posterior distributions
Let’s interpret goby_fit_cov1. Use joint_summarize() to see the posterior summaries of the model parameters.
## mean se_mean sd 2.5% 97.5% n_eff Rhat
## p10 0.003 0.000 0.001 0.001 0.007 18073.87 1
## alpha[1] 0.541 0.001 0.099 0.346 0.737 10482.41 1
## alpha[2] 1.022 0.001 0.118 0.787 1.249 10601.51 1
## alpha[3] -0.350 0.001 0.105 -0.552 -0.141 11073.94 1This summarizes the mean, standard deviation (sd), and quantiles of the posterior estimates of \(p_{10}\) and \(\alpha\), as well as the effective sample size (n_eff) and \(\hat{R}\) (Rhat) for the parameters. More informative about effective sample size and \(\hat{R}\) can be found in the algorithm convergence section, but briefly, the \(\hat{R}\) value is the frequently used statistic for assessing model convergence. We typically want \(\hat{R}\) to be less than 1.05, so it looks like our model converged.
The mean estimated probability of a false positive eDNA detection is 0.001, and the 2.5% and 97.5% quantiles show the bounds of the 95% credibility interval (the equal tailed credibility interval, to be specific.)
The vector \(\alpha\) represents the regression covariates that scales this relationship (see model description for more). alpha[1] corresponds to the intercept of the regression with site-level covariates. alpha[2] corresponds to the regression coefficient associated with Filter_time, and alpha[3] corresponds to the regression coefficient associated with Salinity. Positive regression coefficients indicate an inverse relationship between the covariate and eDNA sensitivity. So here, for example, longer filter time means lower eDNA sensitivity, and higher salinity means higher eDNA sensitivity.
In this example, equation 4 in the model description would be:
\[ \beta_i = \alpha_1 + \alpha_2 \times filtertime_i + \alpha_3 \times salinity_i \]
The parameter \(\beta_i\) represents the site-specific sensitivity of eDNA relative to traditional sampling. We use the index \(i\) to reference the sites. For example, here are the first few \(\beta_i\):
## mean se_mean sd 2.5% 97.5% n_eff Rhat
## beta[1] -0.406 0.002 0.167 -0.736 -0.079 9667.566 1
## beta[2] -0.653 0.002 0.187 -1.018 -0.288 9136.890 1
## beta[3] -0.372 0.002 0.176 -0.724 -0.029 10387.755 1
## beta[4] 0.848 0.001 0.109 0.630 1.062 13430.790 1
## beta[5] 0.171 0.001 0.138 -0.101 0.439 11102.033 1
## beta[6] -0.460 0.002 0.221 -0.895 -0.027 9203.115 1We can also use functions from the bayesplot package to examine the posterior distributions and chain convergence.
First let’s look at the posterior distribution for \(p_{10}\).
library(bayesplot)
# plot posterior distribution, highlighting median and 80% credibility interval
mcmc_areas(as.matrix(goby_fit_cov1$model), pars = "p10", prob = 0.8)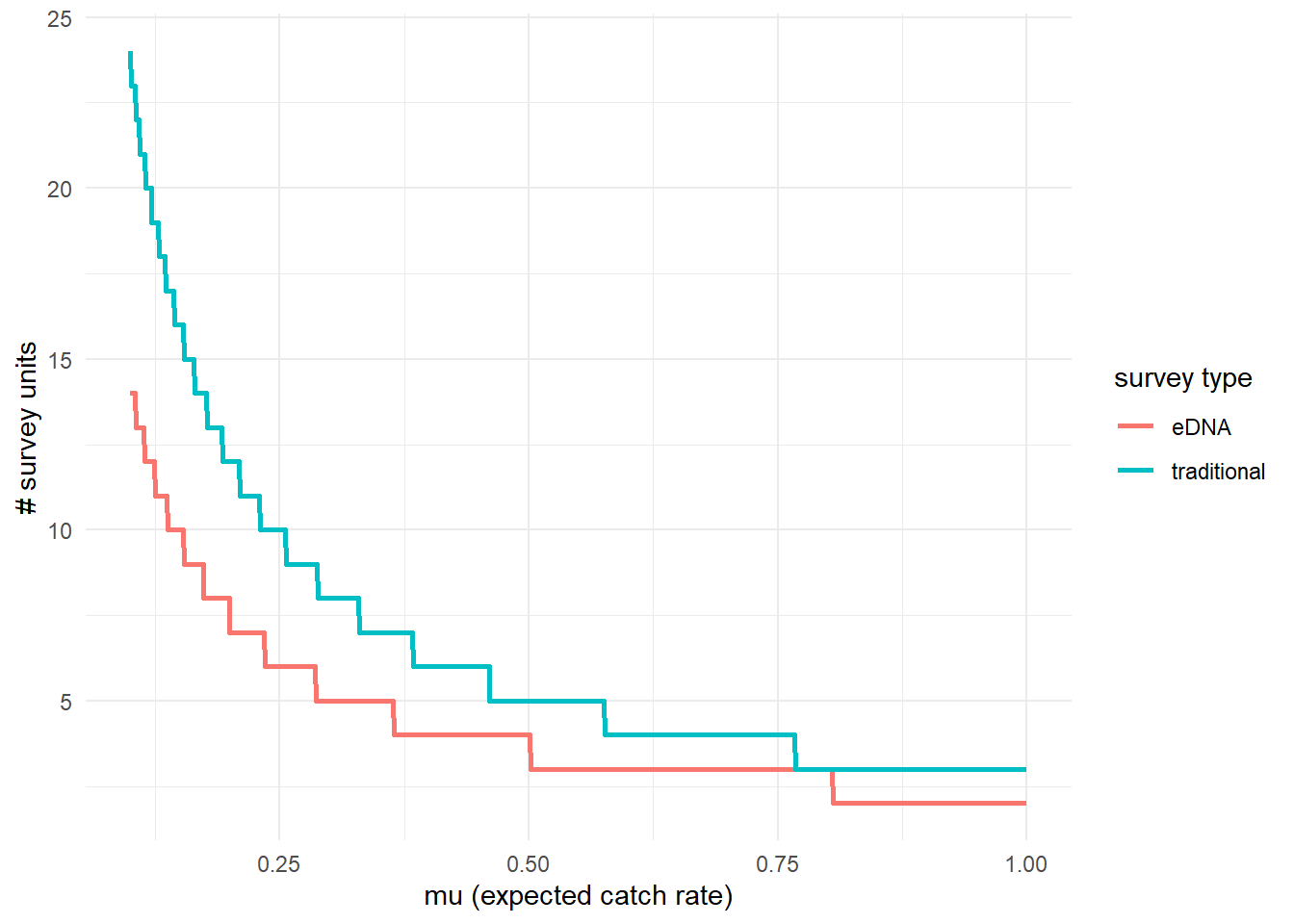
Next let’s look at chain convergence for \(p_{10}\) and \(\mu_{i=1,k=1}\).
# this will plot the MCMC chains for p10 and mu at site 1
mcmc_trace(rstan::extract(goby_fit_cov1$model, permuted = FALSE),
pars = c("p10", "mu[1,1]"))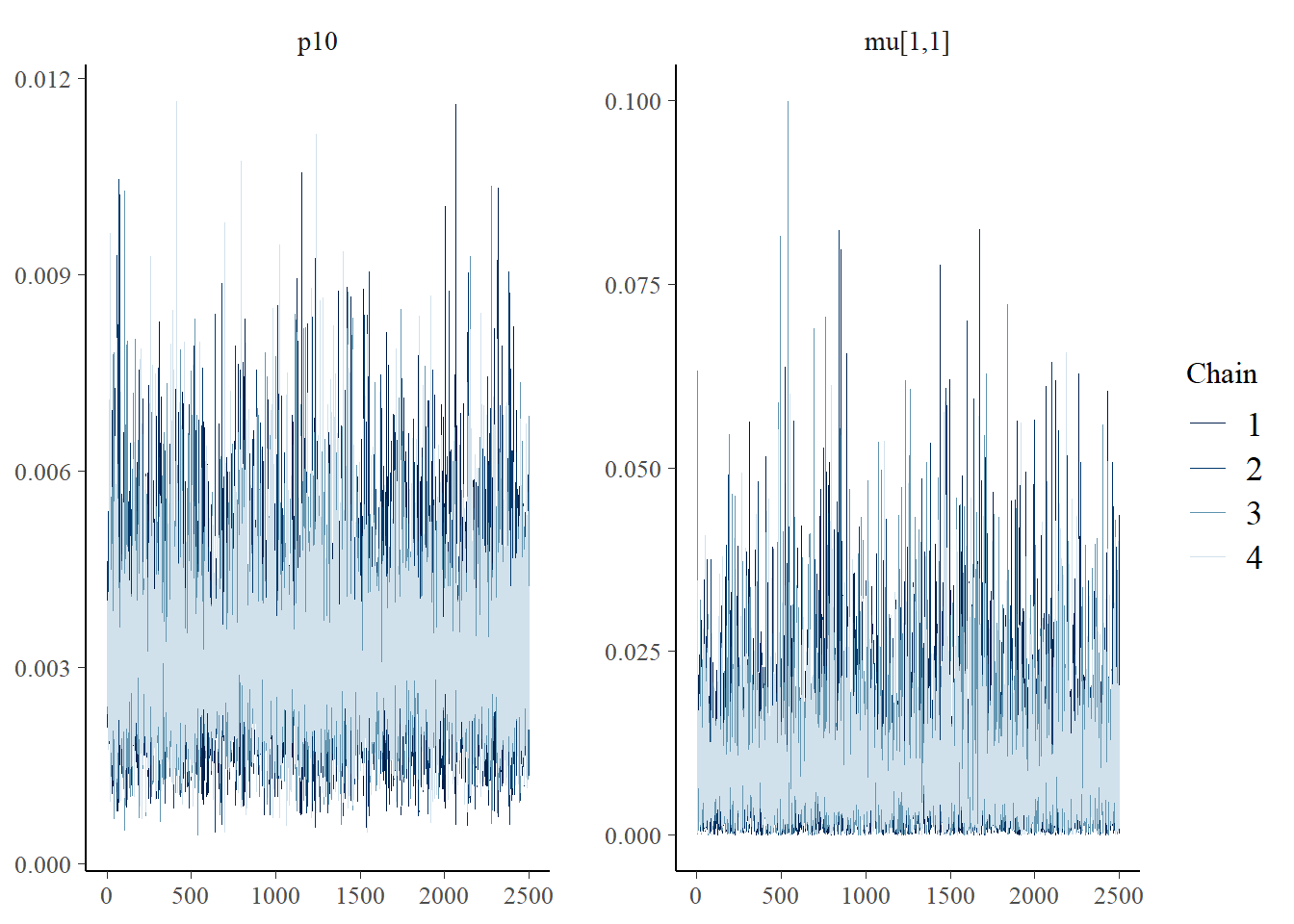
These trace plots show that the algorithm has converged. The chains are overlapping and stationary (i.e., are moving around the same mean and have a constant variance). See more about trace plots in the algorithm convergence section.
4.4.2 Effort necessary to detect presence
To further highlight the relative sensitivity of eDNA and traditional sampling, we can use detection_calculate() to find the units of survey effort necessary to detect presence of the species. Here, detecting presence refers to producing at least one true positive eDNA detection or catching at least one individual in a traditional survey.
This function is finding the median number of survey units necessary to detect species presence if the expected catch rate, \(\mu\) is 0.1, 0.5, or 1. The cov_val argument indicates the value of the covariates used for the prediction. Since the covariate data was normalized, c(0, 0) indicates that the prediction is made at the mean Filter_time and Salinity values. For example, this means that all \(\beta_i = \alpha_1\).
## mu n_traditional n_eDNA
## [1,] 0.1 24 14
## [2,] 0.5 5 4
## [3,] 1.0 3 2We can see that at the mean covariate values, it takes 14 eDNA samples or 24 seine samples to detect goby presence with 0.9 probability if the expected catch rate is 0.1.
Now let’s perform the same calculation under a condition where the Filter_time covariate value is 0.5 z-scores above the mean. This means that equation 4 in the model description would be:
\[ \beta_i = \alpha_1 + \alpha_2 \times 0.5 + \alpha_3 \times 0 \]
detection_calculate(goby_fit_cov1$model, mu = c(0.1, 0.5, 1),
cov_val = c(0.5, 0), probability = 0.9)## mu n_traditional n_eDNA
## [1,] 0.1 24 23
## [2,] 0.5 5 5
## [3,] 1.0 3 3At sites with a longer eDNA sample filter time, it would now take 22 eDNA samples or 24 seine samples to detect goby presence if the expected catch rate is 0.1.
Let’s do the same for salinity. This means that equation 4 in the model description would be:
\[ \beta_i = \alpha_1 + \alpha_2 \times 0 + \alpha_3 \times 0.5 \]
detection_calculate(goby_fit_cov1$model, mu = c(0.1, 0.5, 1),
cov_val = c(0, 0.5), probability = 0.9)## mu n_traditional n_eDNA
## [1,] 0.1 24 12
## [2,] 0.5 5 3
## [3,] 1.0 3 2At sites with higher salinity, it would now take 12 eDNA samples or 24 seine samples to detect goby presence if the expected catch rate is 0.1.
We can also plot these comparisons. mu_min and mu_max define the x-axis in the plot.
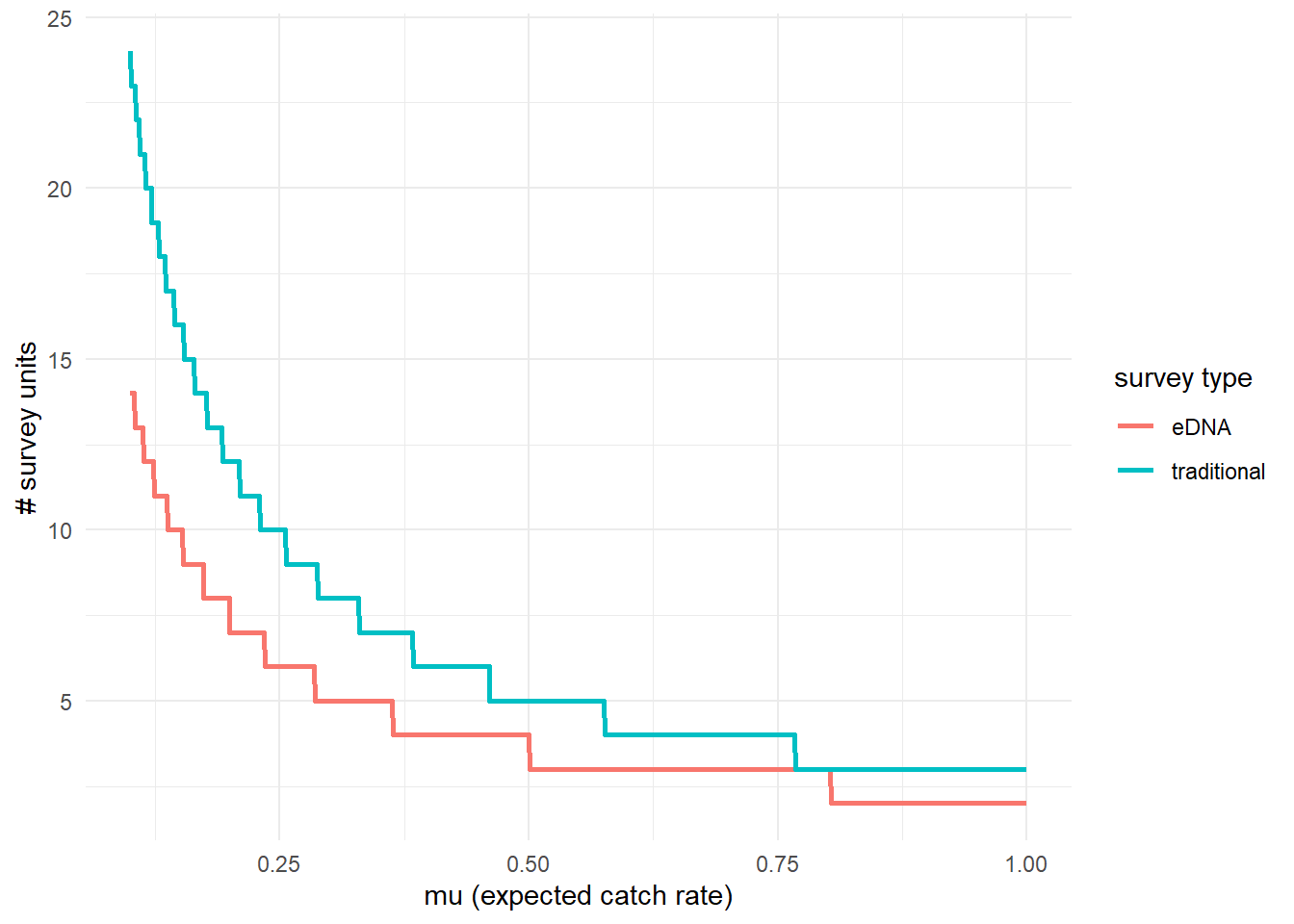
4.4.3 Calculate \(\mu_{critical}\)
The probability of a true positive eDNA detection, \(p_{11}\), is a function of the expected catch rate, \(\mu\). Low values of \(\mu\) correspond to low probability of eDNA detection. Since the probability of a false-positive eDNA detection is non-zero, the probability of a false positive detection may be higher than the probability of a true positive detection at very low values of \(\mu\).
\(\mu_{critical}\) describes the value of \(\mu\) where the probability of a false positive eDNA detection equals the probability of a true positive eDNA detection. This value can be calculated using mu_critical(). Here, we will calculate this value at the mean covariate values.
## $median
## [1] 0.005262879
##
## $lower_ci
## Highest Density Interval: 1.53e-03
##
## $upper_ci
## Highest Density Interval: 9.60e-03This function calculates \(\mu_{critical}\) using the entire posterior distributions of parameters from the model, and ‘HDI’ corresponds to the 90% credibility interval calculated using the highest density interval.
4.5 Initial values
By default, eDNAjoint will provide initial values for parameters estimated by the model, but you can provide your own initial values if you prefer. Here is an example of providing initial values for parameters, mu,p10, and alpha, as an input in joint_model().
# set number of chains
n_chain <- 4
# number of sites
nsites <- dim(goby_data$count)[1]
# initial values should be a list of named lists
inits <- list()
for (i in 1:n_chain) {
inits[[i]] <- list(
# length should equal the number of sites for each chain
mu = stats::runif(nsites, 0.01, 5),
# length should equal 1 for each chain
p10 = stats::runif(1, 0.0001, 0.08),
# length should equal the number of covariates plus 1
# (to account for intercept in regression)
alpha = rep(0.1, length(c("Filter_time", "Salinity")) + 1)
)
}# now fit the model
fit_inits <- joint_model(data = goby_data, cov = c("Filter_time", "Salinity"),
initial_values = inits, multicore = TRUE)## $chain1
## $chain1$mu_trad
## [1] 4.73651091 1.73969524 1.61231249 3.65128178 0.91912270 0.41315891
## [7] 1.93739797 0.70615624 1.28114581 2.01010555 1.91621307 3.81738777
## [13] 4.24071997 0.16963854 4.39636765 2.99997010 3.44395022 4.61554610
## [19] 3.93583065 3.24973296 3.60469682 3.67834965 1.93340631 1.47891091
## [25] 1.82119620 3.31897447 4.99704506 1.22187589 4.71126421 3.60909531
## [31] 1.32820226 2.30448454 0.06530053 3.57328608 0.84835023 2.64391287
## [37] 2.03780080 4.16736431 0.36632083
##
## $chain1$mu
## [1] 4.73651091 1.73969524 1.61231249 3.65128178 0.91912270 0.41315891
## [7] 1.93739797 0.70615624 1.28114581 2.01010555 1.91621307 3.81738777
## [13] 4.24071997 0.16963854 4.39636765 2.99997010 3.44395022 4.61554610
## [19] 3.93583065 3.24973296 3.60469682 3.67834965 1.93340631 1.47891091
## [25] 1.82119620 3.31897447 4.99704506 1.22187589 4.71126421 3.60909531
## [31] 1.32820226 2.30448454 0.06530053 3.57328608 0.84835023 2.64391287
## [37] 2.03780080 4.16736431 0.36632083
##
## $chain1$log_p10
## [1] -3.378982
##
## $chain1$alpha
## [1] 0.1 0.1 0.1
##
## $chain1$p_dna
## numeric(0)
##
## $chain1$p11_dna
## numeric(0)
##
##
## $chain2
## $chain2$mu_trad
## [1] 0.14461142 3.29902766 3.39145517 1.48287580 3.86959463 1.06042273
## [7] 2.32768930 2.44884607 1.40195028 2.37407098 0.40826781 3.21053097
## [13] 2.70556138 3.25324433 1.52512543 2.09494699 2.62512936 0.66401642
## [19] 0.23359237 4.67700038 1.23042655 3.93432191 0.05580183 0.05581739
## [25] 3.86542544 3.07910608 1.12881198 3.59477552 1.79311368 0.56922846
## [31] 0.27567248 2.90127825 4.58146401 4.57097248 1.14137182 3.57060002
## [37] 1.81847216 3.26658495 1.31260469
##
## $chain2$mu
## [1] 0.14461142 3.29902766 3.39145517 1.48287580 3.86959463 1.06042273
## [7] 2.32768930 2.44884607 1.40195028 2.37407098 0.40826781 3.21053097
## [13] 2.70556138 3.25324433 1.52512543 2.09494699 2.62512936 0.66401642
## [19] 0.23359237 4.67700038 1.23042655 3.93432191 0.05580183 0.05581739
## [25] 3.86542544 3.07910608 1.12881198 3.59477552 1.79311368 0.56922846
## [31] 0.27567248 2.90127825 4.58146401 4.57097248 1.14137182 3.57060002
## [37] 1.81847216 3.26658495 1.31260469
##
## $chain2$log_p10
## [1] -2.666832
##
## $chain2$alpha
## [1] 0.1 0.1 0.1
##
## $chain2$p_dna
## numeric(0)
##
## $chain2$p11_dna
## numeric(0)
##
##
## $chain3
## $chain3$mu_trad
## [1] 1.4633128 2.9547527 2.5859346 1.8017323 0.2081068 1.7254861 0.8898845
## [8] 3.1684881 3.9443430 3.9178744 4.8304791 1.3201228 3.3909627 1.5392253
## [15] 2.1486212 0.3184519 1.5771933 0.2524345 0.9593710 4.7791849 2.1560819
## [22] 4.6864184 4.4276737 2.5707206 0.5730558 4.4490581 4.4885246 2.1868134
## [29] 2.3486438 2.8499541 0.1170715 4.3891145 3.8988470 4.4909801 1.5359514
## [36] 4.9679794 4.4671624 4.9034187 0.1302301
##
## $chain3$mu
## [1] 1.4633128 2.9547527 2.5859346 1.8017323 0.2081068 1.7254861 0.8898845
## [8] 3.1684881 3.9443430 3.9178744 4.8304791 1.3201228 3.3909627 1.5392253
## [15] 2.1486212 0.3184519 1.5771933 0.2524345 0.9593710 4.7791849 2.1560819
## [22] 4.6864184 4.4276737 2.5707206 0.5730558 4.4490581 4.4885246 2.1868134
## [29] 2.3486438 2.8499541 0.1170715 4.3891145 3.8988470 4.4909801 1.5359514
## [36] 4.9679794 4.4671624 4.9034187 0.1302301
##
## $chain3$log_p10
## [1] -2.627929
##
## $chain3$alpha
## [1] 0.1 0.1 0.1
##
## $chain3$p_dna
## numeric(0)
##
## $chain3$p11_dna
## numeric(0)
##
##
## $chain4
## $chain4$mu_trad
## [1] 1.7270948 2.8522858 2.2460413 1.9939070 1.2821392 3.0371415 4.0205742
## [8] 0.5875351 2.1766056 4.1799937 4.1626787 1.0571263 3.9630289 0.2472294
## [15] 2.1610957 0.3792458 1.3476875 2.8249661 1.5606263 4.0649165 1.3764974
## [22] 3.4796717 1.4586034 0.6608826 4.0592927 3.7934184 1.3285391 0.5700792
## [29] 1.7953283 0.8794904 0.8204385 1.8677253 2.1144504 2.7462363 1.6110190
## [36] 2.8178140 0.4348132 2.7608918 0.1547004
##
## $chain4$mu
## [1] 1.7270948 2.8522858 2.2460413 1.9939070 1.2821392 3.0371415 4.0205742
## [8] 0.5875351 2.1766056 4.1799937 4.1626787 1.0571263 3.9630289 0.2472294
## [15] 2.1610957 0.3792458 1.3476875 2.8249661 1.5606263 4.0649165 1.3764974
## [22] 3.4796717 1.4586034 0.6608826 4.0592927 3.7934184 1.3285391 0.5700792
## [29] 1.7953283 0.8794904 0.8204385 1.8677253 2.1144504 2.7462363 1.6110190
## [36] 2.8178140 0.4348132 2.7608918 0.1547004
##
## $chain4$log_p10
## [1] -4.787268
##
## $chain4$alpha
## [1] 0.1 0.1 0.1
##
## $chain4$p_dna
## numeric(0)
##
## $chain4$p11_dna
## numeric(0)